Pesas más? Bajas más rápido? La física detrás del ciclismo cuesta abajo
Cuántas veces he oído eso de: «Los que estamos entrados en carnes subimos mal, pero bajamos como misiles». Tenía sentido hasta que en el colegio me contaron la historia de Galileo Galilei. Siempre he sido un firme convencido de que la mejor forma de aprender ciencia es a través de la historia. Galileo demostró que todos los objetos caen al mismo ritmo si ignoramos el rozamiento. Gravedad: g = 9,8 m/s² para todos, sin favoritismos.
Con ese dato, traté de convencer a mis amigos ciclistas: «No bajáis más rápido por pesar más! La gravedad es igual para todos.» Pero nadie me creyó. Y para colmo, la realidad me dejaba en evidencia: los más pesados sí que bajaban más rápido, se veía a simple vista.
Cuando empecé a estudiar Física en la universidad, pedí ayuda a un tutor, también aficionado al ciclismo, para resolver el misterio con cálculos y un poco de ciencia. Por qué los más pesados parecen tener ventaja bajando si la gravedad no discrimina? La respuesta está en algo más que la gravedad: la resistencia aerodinámica y la fuerza gravitatoria.
La clave está en la fuerza gravitatoria y el rozamiento 🚴♂️💨
Para entenderlo, primero hay que aclarar dos conceptos clave:
- Gravedad: La aceleración que produce la gravedad (
) es la misma para todos. Pero la fuerza gravitatoria que actúa sobre un ciclista depende de su masa (
), ya que:
Donde:
: Fuerza gravitatoria (en newtons, N).
: Masa del ciclista (en kg).
: Seno de la pendiente (
).
Los ciclistas más pesados tenemos un mayor, es decir, más fuerza para vencer resistencias.
- Resistencia aerodinámica: En la vida real, el aire actúa como un freno, y es que en ciclismo el aire siempre tiene la culpa de todo. La resistencia aerodinámica está definida por la fórmula:
Donde:
: Fuerza de resistencia aerodinámica (en N).
: Densidad del aire (
).
: Coeficiente de forma (qué tan aerodinámico eres, aprox.
).
: Área frontal del ciclista (en
, aprox. 0.5).
: Velocidad (en
).
Los ciclistas más grandes tenemos un área frontal mayor (), lo que significa más resistencia. Sin embargo, nuestra mayor fuerza gravitatoria (
) compensa este freno.
Ejemplo práctico: yo antes y ahora
Voy a comparar dos versiones de mi mismo:
- En mis días competitivos: 69 kg.
- Actualmente después de navidades: 90 kg.
- Altura antes y ahora: 1,83 m (
).
- Pendiente: 6% (
).
- Velocidad de referencia:
(
).
1. Fuerza gravitatoria (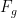 ):
):
Para 69 kg:
Para 90 kg:
2. Resistencia aerodinámica (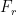 ):
):
Usando la fórmula:
Mis dos yo la misma resistencia aerodinámica, , ya que no depende de la masa y mis michelines aún no sobresalen demasiado.
Diferencia clave:
Mi yo de 90 kg tiene 12.3 N más de fuerza gravitatoria que mi yo de 69 kg. Esto significa que ahora tengo más «empuje» para superar la resistencia aerodinámica. Como resultado, ahora acelero más rápido y mantengo una velocidad mayor, a pesar de que mis dos yo enfrentan el mismo freno del aire.
Conclusión:
- La gravedad no discrimina, pero la fuerza gravitatoria sí: los más pesados tenemos más empuje gracias a la masa.
- La resistencia aerodinámica afecta a todos, pero los más pesados tenemos fuerza suficiente para compensarla.
- Los ciclistas más grandes bajamos más rápido, pero no por tener una gravedad distinta, sino porque nuestra mayor masa nos da ventaja para vencer al aire.
Así que la próxima vez que alguien me diga que bajo más rápido por la gravedad, le corregiré: «No, amigo. Es porque tengo más fuerza para pelearme con el aire.» 🚴♂️💨
De las subidas ya mejor hablamos otro día