Weigh More, Go Faster? The Physics Behind Cycling Downhill
Weigh More, Go Faster? The Physics Behind Cycling Downhill
How many times have I heard: “Those of us who are heavier climb slower but fly downhill like missiles.” It made sense to me until I learned about Galileo Galilei in school. I’ve always believed that the best way to learn science is through stories. Galileo showed that all objects fall at the same rate if we ignore air resistance. Gravity: for everyone, without exceptions.
With this knowledge, I tried to convince my cycling friends: “You don’t go faster downhill just because you weigh more! Gravity is the same for everyone.” But nobody believed me. And to make matters worse, reality proved me wrong: heavier riders were indeed going faster downhill—it was clear to see.
When I started studying physics at university, I asked for help from a tutor who was also a cycling enthusiast to solve the mystery with calculations and some science. Why do heavier riders seem to have an advantage downhill if gravity doesn’t discriminate? The answer lies in more than just gravity: aerodynamic drag and gravitational force.
The Key Lies in Gravitational Force and Air Resistance 🚴♂️💨
To understand this, we first need to clarify two key concepts:
- Gravity: The acceleration produced by gravity (
) is the same for everyone. But the gravitational force acting on a cyclist depends on their mass (
), as:
Where:
: Gravitational force (in newtons, N).
: Mass of the cyclist (in kg).
: Sine of the slope angle (
).
Heavier cyclists have a greater , meaning more force to overcome resistance.
- Aerodynamic drag: In real life, air acts as a brake—and in cycling, air is always to blame. Aerodynamic drag is defined by the formula:
Where:
: Aerodynamic drag force (in N).
: Air density (
).
: Drag coefficient (how aerodynamic you are, approx.
).
: Frontal area of the cyclist (in
, approx. 0.5).
: Velocity (in
).
Heavier cyclists have a larger frontal area (), which means more air resistance. However, their greater gravitational force (
) compensates for this drag.
Practical Example: Me Then and Now
Let’s compare two versions of myself:
- During my competitive days: 69 kg.
- After the holidays: 90 kg.
- Height then and now: 1.83 m (
).
- Slope: 6% (
).
- Reference velocity:
(
).
1. Gravitational Force (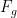 ):
):
For 69 kg:
For 90 kg:
2. Aerodynamic Drag (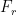 ):
):
Using the formula:
Both versions of me face the same aerodynamic drag, , as it doesn’t depend on mass.
Key Difference:
My 90-kg self has 12.3 N more gravitational force than my 69-kg self. This means I now have more “push” to overcome aerodynamic drag. As a result, I now accelerate faster and maintain a higher speed, even though both versions of me face the same air resistance.
Conclusion:
- Gravity doesn’t discriminate, but gravitational force does: heavier cyclists have more push thanks to their mass.
- Aerodynamic drag affects everyone, but heavier cyclists have enough force to counteract it.
- Heavier cyclists go faster downhill, not because gravity is different, but because their greater mass helps them overcome air resistance.
So, the next time someone tells me I go faster downhill because of gravity, I’ll correct them: “No, my friend. It’s because I have more force to fight the air.” 🚴♂️💨
Let’s talk about climbing some other time!