20 Januar, 2025

Wiegt man mehr, fährt man schneller bergab? Die Physik hinter dem Radfahren bergab

Wie oft habe ich gehört: „Die schwereren von uns fahren bergauf langsam, aber bergab wie Raketen“. Das schien Sinn zu machen, bis ich in der Schule die Geschichte von Galileo Galilei hörte. Ich war schon immer fest davon überzeugt, dass man Wissenschaft am besten durch Geschichten lernt. Galileo zeigte, dass alle Objekte mit der gleichen Geschwindigkeit fallen, wenn man den Luftwiderstand ignoriert. Gravitation: $g = 9,8 \, \text{m/s}^2$ für alle, ohne Ausnahmen.

Mit diesem Wissen versuchte ich, meine Radfahrerfreunde zu überzeugen: „Ihr fahrt nicht schneller bergab, nur weil ihr mehr wiegt! Die Gravitation ist für alle gleich.“ Aber niemand glaubte mir. Und zu allem Überfluss zeigte die Realität: Die Schwereren fuhren tatsächlich schneller bergab – das war nicht zu übersehen.

Als ich begann, Physik an der Universität zu studieren, bat ich einen Tutor, der ebenfalls ein Radfahrer war, um Hilfe, um das Geheimnis mit Berechnungen und etwas Wissenschaft zu lösen. Warum scheinen schwerere Radfahrer bergab einen Vorteil zu haben, obwohl die Gravitation keine Unterschiede macht? Die Antwort liegt in mehr als nur der Gravitation: dem Luftwiderstand und der Gravitationskraft.

Der Schlüssel liegt in der Gravitationskraft und dem Luftwiderstand 🚴‍♂️💨

Um dies zu verstehen, müssen wir zunächst zwei wichtige Konzepte klären:

Gravitation: Die Beschleunigung durch die Gravitation ( $g = 9.8 \, \text{m/s}^2$ ) ist für alle gleich. Aber die Gravitationskraft, die auf einen Radfahrer wirkt, hängt von seiner Masse ( $m$ ) ab, da:

$F_g = m \cdot g \cdot \sin(\theta)$

Wo:

$F_g$ : Gravitationskraft (in Newton, N).
$m$ : Masse des Radfahrers (in kg).
$\sin(\theta)$ : Sinus des Neigungswinkels ( $\theta$ ).

Schwerere Radfahrer haben eine größere $F_g$ , das heißt, sie haben mehr Kraft, um den Widerstand zu überwinden.

Luftwiderstand: In der realen Welt wirkt die Luft wie eine Bremse – und beim Radfahren ist die Luft immer schuld. Der Luftwiderstand wird durch die Formel definiert:

$F_r = \frac{1}{2} \cdot \rho \cdot C_d \cdot A \cdot v^2$

Wo:

$F_r$ : Luftwiderstandskraft (in N).
$\rho$ : Luftdichte ( $\sim 1.2 \, \text{kg/m}^3$ ).
$C_d$ : Formkoeffizient (wie aerodynamisch du bist, ca. $\sim 0.9$ ).
$A$ : Frontalfläche des Radfahrers (in $\text{m}^2$ , ca. 0.5).
$v$ : Geschwindigkeit (in $\text{m/s}$ ).

Schwerere Radfahrer haben eine größere Frontalfläche ( $A$ ), was mehr Luftwiderstand bedeutet. Dennoch kompensiert ihre größere Gravitationskraft ( $F_g$ ) diese Bremse.

Praktisches Beispiel: Ich früher und jetzt

Ich werde zwei Versionen von mir vergleichen:

In meinen Wettkampftagen: 69 kg.
Nach den Feiertagen: 90 kg.
Größe damals und heute: 1,83 m ( $A = 0.5 \, \text{m}^2$ ).
Neigung: 6% ( $\tan(\theta) = 0.06$ ).
Referenzgeschwindigkeit: $v = 10 \, \text{m/s}$ ( $36 \, \text{km/h}$ ).

1. Gravitationskraft (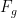 $F_g$ ):

Für 69 kg:

$F_g = 69 \cdot 9.8 \cdot \sin(\arctan(0.06)) \approx 40.5 \, \text{N}$

Für 90 kg:

$F_g = 90 \cdot 9.8 \cdot \sin(\arctan(0.06)) \approx 52.8 \, \text{N}$

2. Luftwiderstand (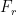 $F_r$ ):

Verwenden der Formel:

$F_r = \frac{1}{2} \cdot 1.2 \cdot 0.9 \cdot 0.5 \cdot (10)^2 = 27 \, \text{N}$

Beide Ichs haben den gleichen Luftwiderstand, $F_r = 27 \, \text{N}$ , da er nicht von der Masse abhängt.

Hauptunterschied:

Mein 90-kg-Ich hat 12.3 N mehr Gravitationskraft als mein 69-kg-Ich. Das bedeutet, dass ich jetzt mehr „Schub“ habe, um den Luftwiderstand zu überwinden. Dadurch beschleunige ich jetzt schneller und halte eine höhere Geschwindigkeit, obwohl beide Ichs dem gleichen Luftwiderstand ausgesetzt sind.

Fazit:

Die Gravitation diskriminiert nicht, aber die Gravitationskraft schon: Schwerere Radfahrer haben mehr Schub dank ihrer Masse.
Der Luftwiderstand wirkt auf alle gleich, aber Schwerere haben genug Kraft, um ihn auszugleichen.
Schwerere Radfahrer fahren schneller bergab, nicht wegen einer anderen Gravitation, sondern weil ihre größere Masse ihnen hilft, die Luft zu durchbrechen.

Wenn mir also jemand sagt, ich fahre schneller bergab wegen der Gravitation, werde ich korrigieren: „Nein, Freund. Es liegt daran, dass ich mehr Kraft habe, um mich mit der Luft anzulegen.“ 🚴‍♂️💨

Über das Bergauffahren reden wir ein anderes Mal!

Radfahren

Nutzloses Wissen, Physik, Radfahren